Semi-Intrusive Stochastic Galerkin Finite Element Method for Adjoint-Based Optimization Under Uncertainty
Published:
Journal of Aerospace Information Systems; Volume 21; Number 9; Year 2024
https://doi.org/10.2514/1.I011254
The stochastic Galerkin method for the propagation of probabilistically modeled uncertainties can be difficult to apply in practice due to its formulation and the challenge of creating a computational infrastructure to support it. To address these challenges, this work proposes a sampling-based stochastic Galerkin method that leverages existing deterministic analysis and adjoint-based derivative implementations. The proposed formulation is semi-intrusive, since it is implemented using an existing deterministic framework, requiring only the numerical sampling of the deterministic residuals, Jacobians, boundary conditions, and adjoint implementations at nodes in the probabilistic domain. The software architectures to support stochastic generalizations of the deterministic finite element frameworks are presented. This proposed approach is demonstrated on a finite-element framework for flexible multibody dynamics problems. Finally, the semi-intrusive implementation of the stochastic Galerkin method is used to demonstrate adjoint gradient-based optimizations of flexible multibody dynamics systems in the presence of probabilistically modeled uncertainties.
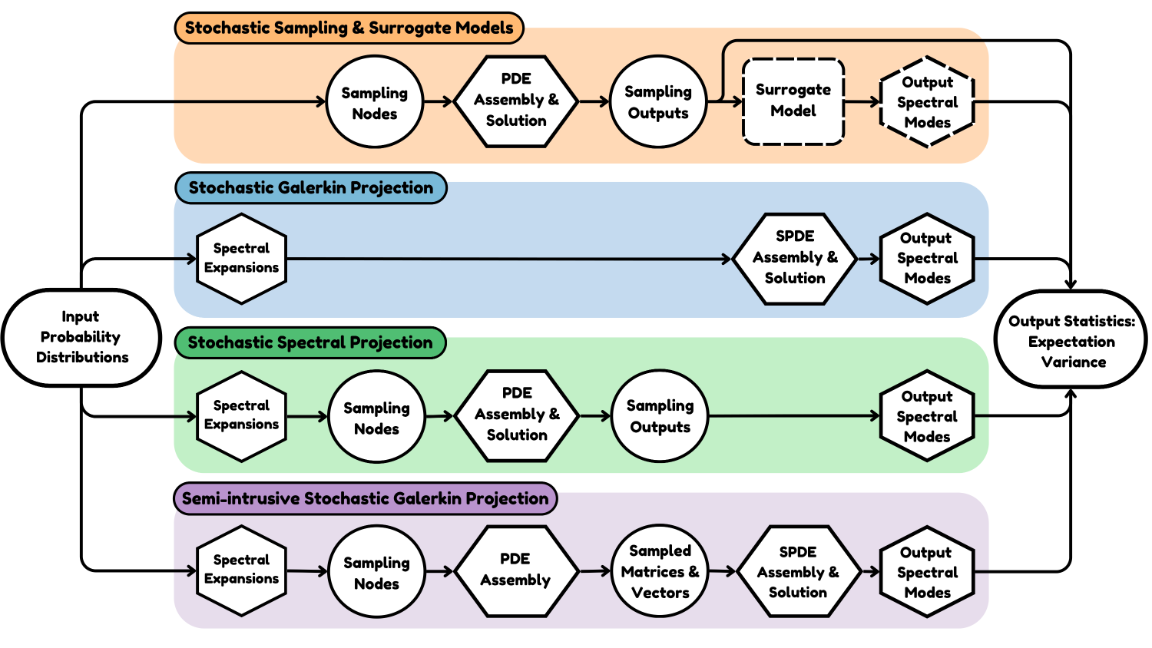
Figure: (1), (3), (4) are the easy to implement sampling-based methods for the propagation of uncertainties through computational physics frameworks.
