Semi-Intrusive Uncertainty Propagation and Adjoint Sensitivity Analysis Using the Stochastic Galerkin Method

22nd AIAA Non-Deterministic Approaches Conference, Orlando, Florida, Jan 2020

https://arc.aiaa.org/doi/10.2514/6.2020-1146

Stochastic Galerkin projection techniques provide an efficient method to propagate uncertainties through simulations governed by differential equations. However, stochastic Galerkin methods are often challenging to implement within existing deterministic finite-element libraries and may require extensive source code modifications. In this work, we present a semi-intrusive stochastic Galerkin methodology that fully reuses existing deterministic finite-element implementations to perform projection in the probabilistic domain. Furthermore, the proposed semi-intrusive technique enables the use of deterministic derivatives for the adjoint method, yielding a stochastic Galerkin adjoint without further implementation effort. The principal idea is to project the deterministic element residuals, Jacobians, boundary conditions, and adjoint terms on to the probabilistic space prior to assembly of the stochastic finite element system, assuming the deterministic implementations to be black-box. The deterministic implementations must support the ability to update random parameters to enable quadrature in the stochastic space. The proposed semi-intrusive stochastic Galerkin approach is demonstrated using TACS, a finite-element framework with a adjoint-based gradient evaluation methods. The capabilities are demonstrated on several test problems including a flexible multibody dynamics simulation of a four bar mechanism.

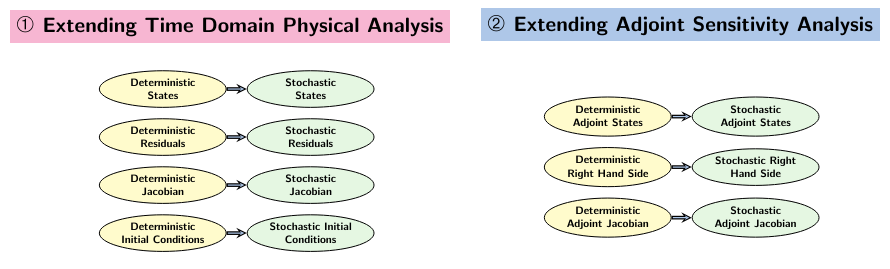
Figure: The applied conceptual framework for a probablistic sampling based stochastic Galerkin implementation.